动态规划—背包问题（Python）

发表： 分类： 本文字数： 1.7k 阅读时长 ≈ 2 分钟

一、什么是动态规划（Dynamic Programming，DP）

  • 1.动态规划是通过组合子问题的解来解决原问题
  • 2.动态规划应用于子问题重叠的情况，即不同的子问题具有公共的子子问题
  • 3.动态规划算法对每个子子问题只求解一次
  • 4.动态规划通常用来求解最优化问题
    注：每个子问题必须是离散的，没有依赖关系，比如要解决子问题1 必须通过解决子问题2 才可以解决。

二、背包问题

  问题描述：将四个不同重量不同价值的物品放入一个背包，使得背包中的物品价值总和最大。例如，

物品 重量 价值
音响 4 3000
电脑 3 2000
吉他 1 1500
手机 1 2000
将以上物品怎样放入一个载重为4的背包可以获得最大价值，求最优解。

三、DP算法思路

1、传统思路

  传统思路是将不同物品进行排列组合放入背包，通过比较全部的组合形式以获得最优解，而这种算法是时间复杂度是指数级别，后果就是当子问题越多时计算量将会急剧增长。

2、DP算法思路

  DP算法是将主问题分解成若干小问题，自下而上求解子问题。
在这里通过将背包容量分割以及不同物品组成网格，每一行物品将对应的网格填充并比较上一行的价值大小。如下：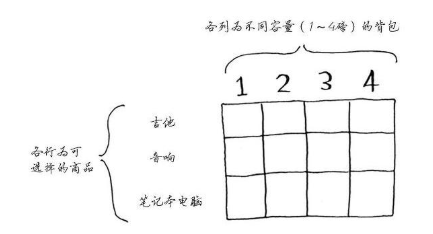

具体思路看参考链接。

四、代码例程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 这里使用了图解中的吉他，音箱，电脑，手机做的测试，数据保持一致
w = [0, 1, 4, 3, 1]   #n个物体的重量(w[0]无用)
p = [0, 1500, 3000, 2000, 2000]   #n个物体的价值(p[0]无用)
n = len(w) - 1   #计算n的个数
m = 4   #背包的载重量

x = []   #装入背包的物体，元素为True时，对应物体被装入(x[0]无用)
v = 0
#optp[i][j]表示在前i个物体中，能够装入载重量为j的背包中的物体的最大价值
optp = [[0 for col in range(m + 1)] for raw in range(n + 1)]
#optp 相当于做了一个n*m的全零矩阵的赶脚，n行为物件，m列为自背包载重量

def knapsack_dynamic(w, p, n, m, x):
    #计算optp[i][j]
    for i in range(1, n + 1):       # 物品一件件来
        for j in range(1, m + 1):   # j为子背包的载重量，寻找能够承载物品的子背包
            if (j >= w[i]):         # 当物品的重量小于背包能够承受的载重量的时候，才考虑能不能放进去
                optp[i][j] = max(optp[i - 1][j], optp[i - 1][j - w[i]] + p[i])    # optp[i - 1][j]是上一个单元的值， optp[i - 1][j - w[i]]为剩余空间的价值
            else:
                optp[i][j] = optp[i - 1][j]
    
    #递推装入背包的物体,寻找跳变的地方，从最后结果开始逆推
    j = m
    for i in range(n, 0, -1):
        if optp[i][j] > optp[i - 1][j]:
            x.append(i)
            j = j - w[i]  
    
    #返回最大价值，即表格中最后一行最后一列的值
    v = optp[n][m]
    return v
 
print '最大值为：' + str(knapsack_dynamic(w, p, n, m, x))
print '物品的索引：',x

#最大值为：4000
#物品的索引： [4, 3]

参考链接

动态规划(DP)的整理-Python描述